Author: Marco Stiegelmaier
Some security algorithms like ECDSA used within certain scenarios are highly recommended by organizations like the National Institute of Standards and Technology (NIST) or the german Federal Office for Security in information Technology (BSI).
The problem with these recommendations is, that they have to be utilized appropriately and with a decent knowledge of crucial relationships between e.g. signatures, randomness and the potential revelation of the private key.
So here is an exciting example what might happen, if the randomness used for creating a digital signature with ECDSA is insufficient:
I created a test certificate based on Elliptic Curve Cryptography. Afterwards I signed two different messages utilizing ECDSA with SHA256. For the 128 bit randomness I leveraged the Python random module. A special Python Lattice modul does the job finally. The private key was completely revealed.
Look what happened to my private key:
Lattice ECDSA Attack
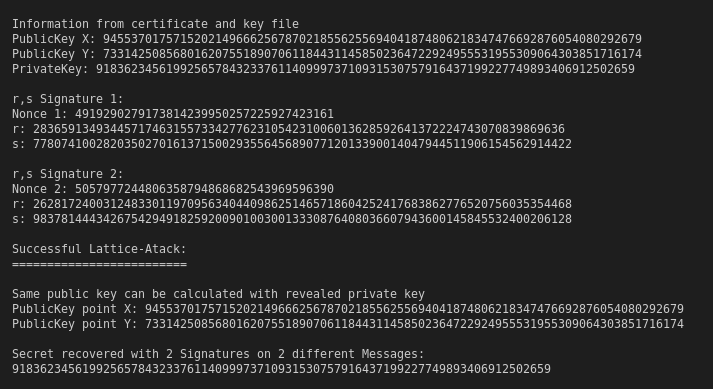
So now please don’t panic. Neither this becomes a reason no longer using ECDSA nor it is a reason challenging any existing implementation.
If your implementation is compliant to the RFC6979 which deals with quality of randomness, you can completely calm down.
If you are interested in playing around with this kind of stuff, feel free to use this Python script on the bottom of this page.
Try it out using Python 3.x
import random
from ecdsa import NIST256p
from ecdsa.ecdsa import Public_key, Private_key
import libnum
import hashlib
from cryptography.x509 import load_pem_x509_certificate
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives.serialization import load_pem_private_key
import olll
gen = NIST256p.generator
order = gen.order()
certificate_pem = b'-----BEGIN CERTIFICATE-----\n\
MIICIjCCAcigAwIBAgIILn88CqXhfhwwCgYIKoZIzj0EAwIwaTELMAkGA1UEBhMC\n\
REUxFjAUBgNVBAgTDU5pZWRlcnNhY2hzZW4xEDAOBgNVBAcTB0dpZmhvcm4xEzAR\n\
BgNVBAoTClByaXZhdGVPcmcxGzAZBgNVBAMTEk1hcmNvIFN0aWVnZWxtYWllcjAe\n\
Fw0yMTExMjgxMTEyMDBaFw0yMjExMjgxMTEyMDBaMGkxCzAJBgNVBAYTAkRFMRYw\n\
FAYDVQQIEw1OaWVkZXJzYWNoc2VuMRAwDgYDVQQHEwdHaWZob3JuMRMwEQYDVQQK\n\
EwpQcml2YXRlT3JnMRswGQYDVQQDExJNYXJjbyBTdGllZ2VsbWFpZXIwWTATBgcq\n\
hkjOPQIBBggqhkjOPQMBBwNCAATRC3+pR2eC/kmeFx/oIGCiItxpKD0hsJiFcb+v\n\
r6SHR6IWZT4cY15yJKRuCSJNNnHxQHoYjt2J5Ybl84R+wb5Oo1owWDAJBgNVHRME\n\
AjAAMB0GA1UdDgQWBBRxRDp2qXuEYXQRzKdpB3TvzhEhQDAfBgNVHSMEGDAWgBRx\n\
RDp2qXuEYXQRzKdpB3TvzhEhQDALBgNVHQ8EBAMCBeAwCgYIKoZIzj0EAwIDSAAw\n\
RQIgc8sEnU4Px1Q67SgwqXBpUsdsY7kFaMIg9DEoH6DLMn0CIQDubfFS6VkWFrfo\n\
7c6+6o96/s3CqPif3h18u0wUU9fqdw==\n\
-----END CERTIFICATE-----'
private_key_pem = b'-----BEGIN EC PRIVATE KEY-----\n\
MHcCAQEEIMsJd3zu40s5dqlihHCkc9oSvMZfFaAb4U2fvFdLeVuDoAoGCCqGSM49\n\
AwEHoUQDQgAE0Qt/qUdngv5Jnhcf6CBgoiLcaSg9IbCYhXG/r6+kh0eiFmU+HGNe\n\
ciSkbgkiTTZx8UB6GI7dieWG5fOEfsG+Tg==\n\
-----END EC PRIVATE KEY-----'
#Get the certificate for determining the x and y coordinates of the public key
certificate = load_pem_x509_certificate(certificate_pem, default_backend())
pub_key_x = certificate.public_key().public_numbers().x
pub_key_y = certificate.public_key().public_numbers().y
#Get the private key
private_key_temp = load_pem_private_key(private_key_pem, None)
secret = private_key_temp.private_numbers().private_value
#Shift to different library for demonstration purposes (ECDSA)
pub_key = Public_key(gen, gen * secret)
priv_key = Private_key(pub_key, secret)
print("\n\nInformation from certificate and key file")
print("PublicKey X:", pub_key.point.x())
print("PublicKey Y:", pub_key.point.y())
print ("PrivateKey:",secret)
#128 bit random value for the signature algorithm
nonce1 = random.randrange(1, 2**127)
nonce2 = random.randrange(1, 2**127)
#Create two different signatures based on two different messages
message_1 = b'Hello Security Community!'
message_2 = b'Hello Hacking Community!'
hash = hashlib.sha256()
hash.update(message_1)
message1 = hash.digest()
hash = hashlib.sha256()
hash.update(message_2)
message2 = hash.digest()
signature1 = priv_key.sign(int.from_bytes(message1, byteorder="big"), nonce1)
signature2 = priv_key.sign(int.from_bytes(message2, byteorder="big"), nonce2)
#Output the signatures together with the used nonce
print("\nr,s Signature 1:")
print("Nonce 1:", nonce1)
print("r:", signature1.r)
print("s:", signature1.s)
print("\nr,s Signature 2:")
print("Nonce 2:", nonce2)
print("r:", signature2.r)
print("s:", signature2.s)
#Delete the private key from memory
del private_key_temp
del priv_key
#Proceed just using the signatures and messages
r1 = signature1.r
s1_inv = libnum.invmod(signature1.s, order)
r2 = signature2.r
s2_inv = libnum.invmod(signature2.s, order)
s1 = signature1.s
r1_inv = libnum.invmod(signature1.r, order)
matrix = [[order, 0, 0, 0], [0, order, 0, 0],
[r1*s1_inv, r2*s2_inv, (2**128) / order, 0],
[int.from_bytes(message1, byteorder="big")*s1_inv, int.from_bytes(message2, byteorder="big")*s2_inv, 0, 2**128]]
new_matrix = olll.reduction(matrix, 0.75)
for row in new_matrix:
potential_nonce_1 = row[0]
potential_priv_key = r1_inv * ((potential_nonce_1 * s1) - int.from_bytes(message1, byteorder="big"))
if Public_key(gen, gen * potential_priv_key).point.x() == pub_key_x:
print("\nSuccessful Lattice-Atack:")
print("=========================")
print("\nSame public key can be calculated with revealed private key")
print("PublicKey point X:", Public_key(gen, gen * potential_priv_key).point.x())
print("PublicKey point Y:", Public_key(gen, gen * potential_priv_key).point.y())
print("\nSecret recovered with 2 Signatures on 2 different Messages:")
print(potential_priv_key.__divmod__(order)[1])